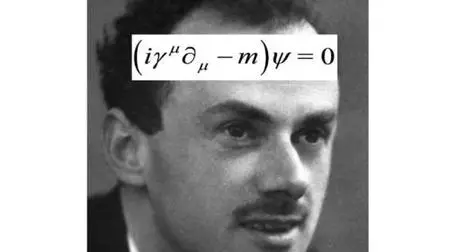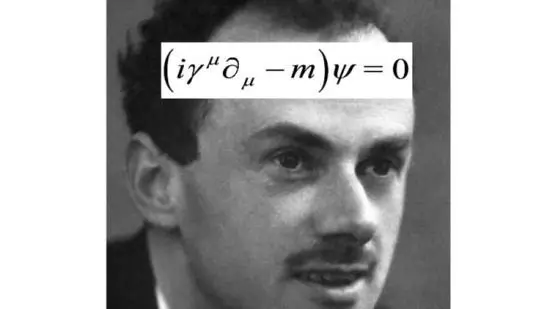Math Intuition for Quantum Mechanics & Quantum Field Theory

Quantum Mechanics and Quantum Field Theory

What you'll learn:
The mathematical intuition for Quantum Mechanics and Quantum field theory
How to (intuitively) derive the Schrodinger's equation from the classical theory
Quantum operators
Quantum states
Importance of commutators
Derivation of Heisenberg Uncertainty Principle
Unitary operators
How to quantize a Classical Field theory
Klein Gordon equation
Wick's theorem
Time ordering
Normal ordering
Noether's theorem
Properties of the infinitesimal Lorentz transformation
Spectrum of the Hamiltonian
Scattering cross-section
Annihilation and creation operators
Causality in quantum field theories
Ground state
Green functions
Schrodinger's picture
Heisenberg's picture
Interaction picture
Theory of Fermions
Theory of Bosons
Dirac equation
Interacting Field theory
Feynman diagrams
Anomalous magnetic moment

Requirements
Special Relativity (for Quantum Field Theory)
Fourier Series and Transforms
Multivariable Calculus
Tensors (for Quantum Field Theory)
Complex calculus (for Quantum Field Theory)
Classical Physics
Probability theory (distributions, probability densities, etc.)

Description
This course aims to mathematically motivate both Quantum Mechanics (QM) and Quantum field Theory (QFT). The first part is devoted to the most important concepts and equations of QM, whereas the second part deals with QFT.

Due to the conceptual and mathematical difficulty of these subjects, some prerequisites to this course are unavoidably required. The student should be familiar with:

1) the Fourier Series and Transform;

2) Multivariable Calculus;

3) Probability theory and random variables;

4) Classical Physics;

5) Complex Calculus (especially residues and calculation of integrals on a contour), although this is necessary only for some parts of the course devoted to QFT;

6) Special Relativity and tensors for QFT.

Note 1: the first few prerequisites might be enough if you are interested only in the first part of the course, which is related to QM (consider that this course has tens of hours' worth of material, you might be interested only in some parts);

Note 2: I'm more than willing to reply if you have doubts/need clarifications, or -why not- have any recommendations to improve the quality of the course.

Note 3: I'll still keep editing the videos (for example by adding notes) to make the video-lectures as clear as possible.

The references for the part on QFT are the following:

- Quantum Field Theory, M.Srednicki

- Quantum Field Theory, Itzykson & Zuber

- QFT by Mandl & Shaw

- QFT in a nutshell, A.Zee

- QFT by Ryder, Ramand

- The Quantum Theory of Fields, S.Weinberg

- Gauge Theories in Particle Physics, Aitchison & Z.Hey

Who this course is for
Students who desire to develop mathematical intuition for Quantum mechanics and Quantum Field theory