Mathematical Foundation for AI and Machine Learning
MP4 | Video: MPEG-4 1920x1080 | Audio: AAC, 44.1 KHz @ 128 Kbps 2ch
Duration: 4.25 hours | Language: English | 690 MB
Genre: eLearning Video / Development / Programming
MP4 | Video: MPEG-4 1920x1080 | Audio: AAC, 44.1 KHz @ 128 Kbps 2ch
Duration: 4.25 hours | Language: English | 690 MB
Genre: eLearning Video / Development / Programming
Learn the core mathematical concepts for machine learning and learn to implement them in R and Python. Artificial Intelligence has gained importance in the last decade with a lot depending on the development and integration of AI in our daily lives. The progress that AI has already made is astounding with innovations like self-driving cars, medical diagnosis and even beating humans at strategy games like Go and Chess.
The future for AI is extremely promising and it isn’t far from when we have our own robotic companions. This has pushed a lot of developers to start writing codes and start developing for AI and ML programs. However, learning to write algorithms for AI and ML isn’t easy and requires extensive programming and mathematical knowledge. Mathematics plays an important role as it builds the foundation for programming for these two streams. And in this course, we’ve covered exactly that. We designed a complete course to help you master the mathematical foundation required for writing programs and algorithms for AI and ML.
Style and Approach
The course has been designed in collaboration with industry experts to help you breakdown the difficult mathematical concepts known to man into easier to understand concepts.The course covers three main mathematical theories: Linear Algebra, Multivariate Calculus and Probability Theory.
What You Will Learn in Mathematical Foundation for Artificial Intelligence and Machine Learning
- Refresh the mathematical concepts for AI and Machine Learning
- Learn to implement algorithms in Python
- Understand the how the concepts extend for real-world ML problems
INTRODUCTION
LINEAR ALGEBRA
MULTIVARIATE CALCULUS
PROBABILITY THEORY
PROBABILITY THEORY
- Introduction
LINEAR ALGEBRA
- Scalars, Vectors, Matrices, and Tensors
- Vector and Matrix Norms
- Vectors, Matrices, and Tensors in Python
- Special Matrices and Vectors
- Eigenvalues and Eigenvectors
- Norms and Eigendecomposition
MULTIVARIATE CALCULUS
- Introduction to Derivatives
- Basics of Integration
- Gradients
- Gradient Visualization
- Optimization
PROBABILITY THEORY
- Intro to Probability Theory
- Probability Distributions
- Expectation, Variance, and Covariance
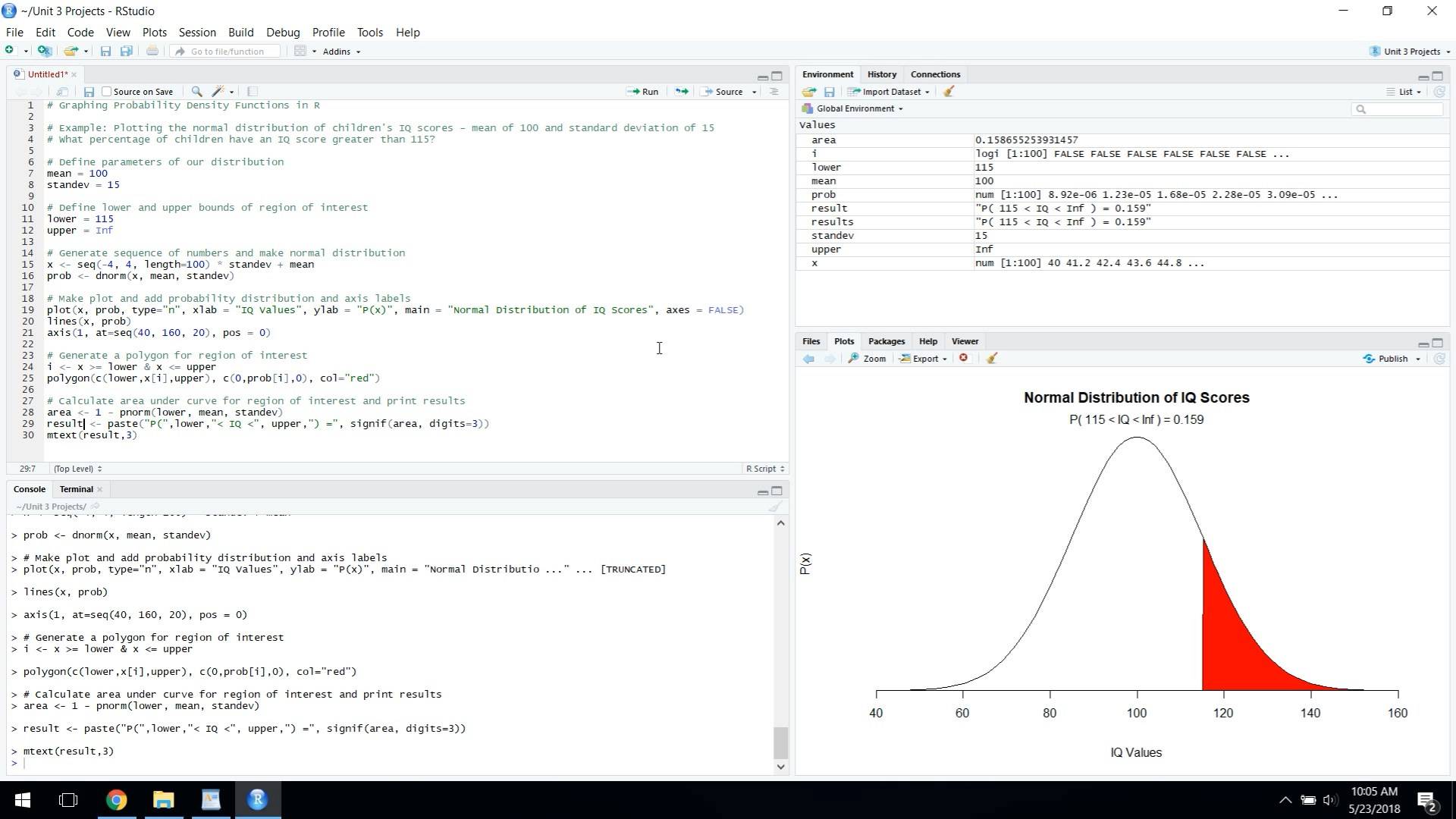
- Graphing Probability Distributions in R
- Covariance Matrices in R
PROBABILITY THEORY
- Special Random Variables