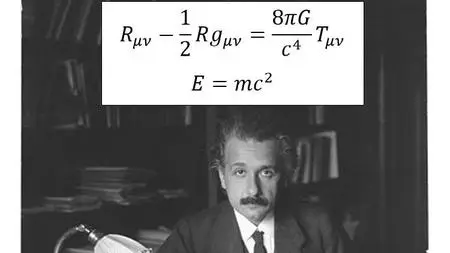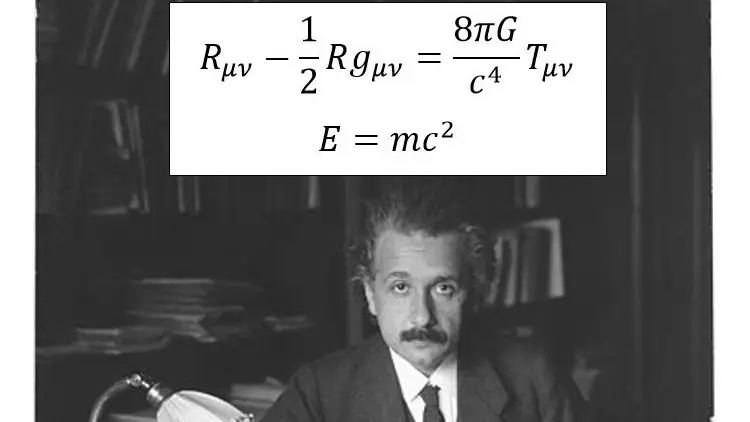Mathematical intuition behind Special and General Relativity
.MP4, AVC, 1280x720, 30 fps | English, AAC, 2 Ch | 11h 31m | 13.58 GB
Instructor: Emanuele Pesaresi
.MP4, AVC, 1280x720, 30 fps | English, AAC, 2 Ch | 11h 31m | 13.58 GB
Instructor: Emanuele Pesaresi
What you'll learn
Special Relativity
General Relativity
Lagrangian mechanics
tensors
Lorentz transformations
time dilation
length contraction
field equations
how to construct a Lagrangian
geodesics
equivalence principle
covariant formulation of physics
covariant derivatives
how to motivate EVERY equation in Special and General Relativity
proof of E=mc^2
why photons have momentum
Requirements
Multivariable Calculus (derivatives, integrals, Divergence theorem, vectors, matrix multiplication, determinants)
Classical mechanics (Newton's laws, kinetic energy, potential, Galileo's transformations)
Maxwell's equations (even a basic knowledge could be enough)
Description
This course starts from the incompatibility between Galileo's principle and Maxwell's equations, and expands on that in order to consistently formulate Special Relativity and later on, in the second part of the course, General Relativity. The other main purpose is to stimulate students to develop the mathematical intuition required to fully grasp and appreciate the contents of these subjects. Therefore, EVERY equation in this course will be motivated. Besides, other key concepts such as: Lagrangian mechanics (i.e. the Action Principle, Lagrange equations), tensors, will be fully covered in the course. The main prerequisites to the course are Calculus and Multivariable Calculus, especially: the divergence theorem, vectors, dot and cross products, matrix multiplication, determinants. Some (basic) knowledge of Classical physics is recommended, such as: scalar potential, Newton laws, Kinetic energy, Energy conservation, Wave equation (and I mean just the mathematical form of the equation).
In the first part of the course Lorentz transformations are derived in two different ways. The mathematics to be able to follow this part can be more easily digested than the mathematics required to follow the part on General Relativity. For General Relativity, it is recommended to follow along with a piece of paper and pencil and derive the equations. Please make sure that you meet the prerequisite requirements.
Who this course is for:
students who want to motivate EVERY equation constituting the foundations of both Special and General Relativity
students who aim to obtain a thorough understanding of the Lagrangian formulation of Physics
students interested in learning tensors
students who desire to learn Special Relativity
students who desire to learn General Relativity