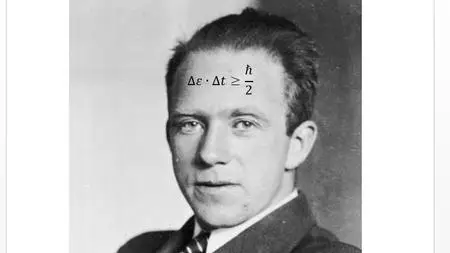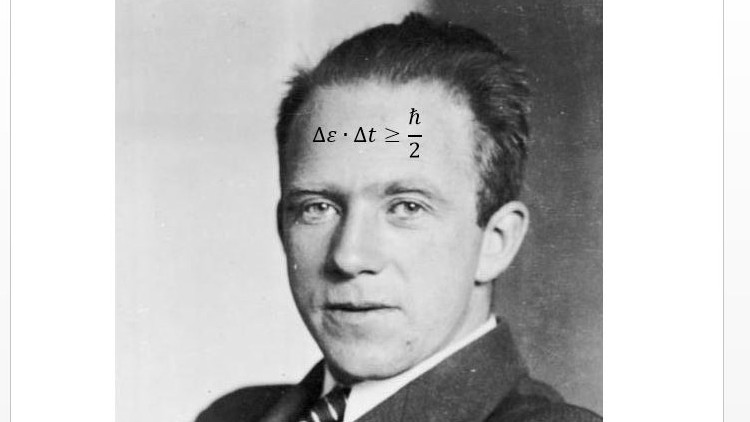Mathematical intuition for Heisenberg Uncertainty Principle

Why particles can come into existence and then fall back into non-existence

What you'll learn

How to derive Heisenberg Uncertainty Principle using concepts of Probability Theory

Requirements

Fourier Transform and its Inverse
Some notions of probability theory (distributions, mean, variance)
Calculus (Integration by parts, derivatives)
Complex numbers

Description

This course revolves around the mathematical derivation of Heisenberg Uncertainty Principle. Starting from some intuitive assumptions about probability distributions, we will derive this famous principle (which becomes a theorem starting from the axioms of probability). We will also dedicate some time to the physical insights and implications of this principle, such as the possibility that particles can come into existence and fall back into non-existence.

The prerequisites to the course are:

-knowledge of what probability distributions are
-how to calculate the mean and the variance of a random variable from a probability distribution
-the definition of the Fourier Transform and its Inverse Transform
-integration by parts and how to take derivatives

Who this course is for:

Students who are interested in Physics and in mathematical derivations of concepts