TTC Video - Mathematical Brain Teasers and Logic Puzzles
.MP4, AVC, 1280x720, 30 fps | English, AAC, 2 Ch | 5h 11m | 4.36 GB
Lecturer: Jason Rosenhouse , PhD Professor, James Madison University | Course No. 9076
.MP4, AVC, 1280x720, 30 fps | English, AAC, 2 Ch | 5h 11m | 4.36 GB
Lecturer: Jason Rosenhouse , PhD Professor, James Madison University | Course No. 9076
Brain teasers are fun and popular activities for all ages and all levels of reasoning skill. For example, here’s a good one: A man goes into a store to buy a certain item. The clerk tells him the item costs 25¢ each. The man replies, “Great, I’ll take 100.” The clerk charges him 75¢. What was the man buying? Here, the solution involves thinking outside the box, in which you approach the problem from a new perspective, often by paying close attention to ambiguity in how the problem is stated. Thinking outside the box is a great strategy for many situations in life.
Here’s another: On the Island of Knights and Knaves, knights always tell the truth and knaves always lie. Two residents of the island walk up to you and one says, “Both of us are knaves.” What can you conclude? This is a classic logic exercise, requiring you to sort through different possibilities and deduce what must be the case, given the information available. Some facility for logical reasoning is another great habit to cultivate.
Research shows that amusing yourself with brain teasers and logic puzzles is an excellent way to sharpen your mind, increase critical thinking skills, and boost creativity. In addition, these entertaining exercises often have deep connections to mathematics, which helps explain why many professional mathematicians start out as youngsters fascinated with puzzles.
In Mathematical Brain Teasers and Logic Puzzles, award-winning teacher and puzzle master Dr. Jason Rosenhouse, Professor of Pure Mathematics at James Madison University, introduces you to a selection of his all-time favorite mind-benders, including some going back to his childhood. Practically all of his 12 half-hour lessons start with a relatively simple problem that demonstrates a mathematical idea or problem-solving strategy. From there, you head deeper into the weeds, venturing into territory that will give you hours of challenging cogitation. While these puzzles can feel complicated on the surface, actually, no skills beyond middle school math are required.
Test Your Wits, Logic, and Persistence
Professor Rosenhouse starts the course by noting that despite all the difficulties humans face, they delight in inventing new problems solely for the pleasure of solving them. After speculating why that might be, he gets down to business—and fun. He introduces several classic puzzles that led to entirely new fields of mathematics. For example, in the 18th century, the city of Königsberg in Prussia had seven bridges connecting two islands with the surrounding city. Curious minds wondered whether it was possible to undertake a walk around Königsberg in such a way as to cross each bridge exactly once. With two islands to worry about and with so many possible walks, this problem is hard to solve just by walking around the city. The great mathematician Leonhard Euler finally answered the question, and in the process laid the foundation for graph theory.
Suitably inspired, you will plunge into more accessible—but no less beguiling—problems, including puzzles like these:
Original Outside-the-Box Puzzle: Nine dots arrayed in a square form the iconic outside-the-box puzzle. The goal is to connect all the dots with four straight lines without lifting your pencil from the page. In fact, by thinking really outside the box, it’s possible to connect the dots with just three lines.
140 Legs in a Barn: A barn holds a combined total of 50 chickens and horses. Altogether there are 140 legs. How many chickens and how many horses are there? You may be tempted to use algebra to reach a solution, but there is a much simpler way you can do quickly in your head. Can you see it?
Can Logic Get You into Heaven? You face two unmarked doors: one leading to heaven, the other to hell. A guard stands in front of each door. One is an always truthful knight, the other an always deceitful knave. You don’t know which is which. What single yes/no question can you ask to reveal the door to paradise?
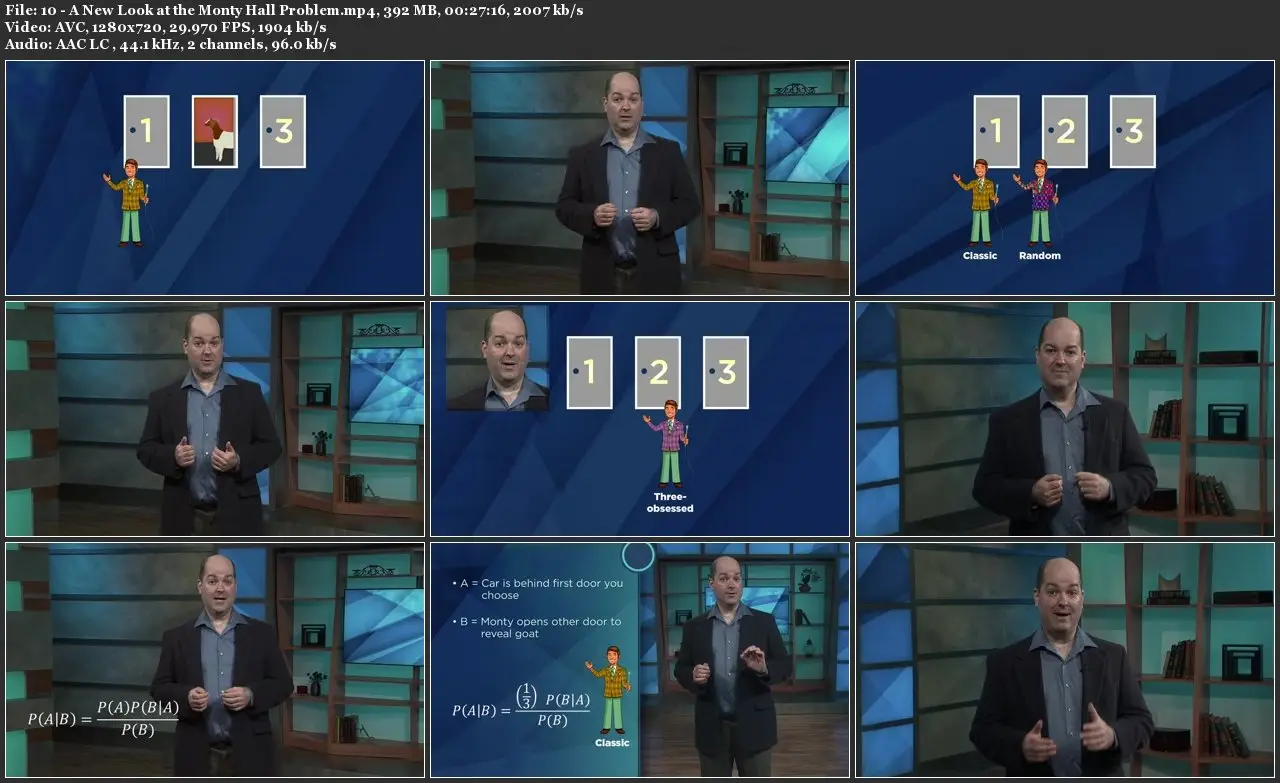
Monty Hall Problem: Professor Rosenhouse analyzes the probability of different versions of the famous Monty Hall problem, in which the quizmaster of Let’s Make a Deal offers you a chance to switch your original choice after he reveals hidden information. A new car hinges on your decision!
Wolf, Goat, Cabbage: You must transport a wolf, a goat, and a cabbage across a river. You can carry only one of them at a time. However, the wolf will eat the goat if they are left unattended. Likewise, the goat will eat the cabbage. This puzzle is 1,200 years old, but its solution reflects the sort of algorithmic thinking underlying modern computer science.
The Joy of Figuring It Out
You also confront the so-called “Hardest Logic Puzzle Ever,” which lives up to its name. You delve into brain teasers devised by the celebrated Raymond Smullyan, inventor of “knights and knaves” and other logic challenges. You dip into Lewis Carroll’s diverting exercises in Aristotelian logic. You get to the heart of the paradoxical Tuesday birthday problem. You discover the connection between a horse on a treadmill and transcontinental air travel. You put yourself in the shoes of muddy-faced children who must determine, without mirrors or other obvious clues, that their faces are indeed muddy. And much more.
Professor Rosenhouse also provides useful tips for solving puzzles, including this observation for the muddy children problem: “Sometimes you have more information than you think. With careful attention to detail and a lot of patience and clear thinking, you can accomplish quite a lot from a very minimal starting point.” That’s good advice for any problem in life!
Throughout Mathematical Brain Teasers and Logic Puzzles, you learn useful ideas in mathematics and logic, such as:
Conditional and biconditional statements;
Coercive logic;
Conditional probability;
Why multiplying two negative numbers gives a positive result;
Bayes’ theorem;
Algorithmic thinking, and many other concepts.
But the biggest payoff is sheer joy. “A well-crafted puzzle or a clever brainteaser can be a lot of fun,” says Professor Rosenhouse, “and when you solve one, it can bring a smile to your face for the rest of the day.”
(Answer to the puzzle in the first paragraph: The man was buying house numbers. He paid 75 cents for numbers 1, 0, and 0. For solutions to the other puzzles, watch Mathematical Brain Teasers and Logic Puzzles. You’ll be inspired and amazed!)
Research shows that amusing yourself with brain teasers and logic puzzles is an excellent way to sharpen your mind, increase critical thinking skills, and boost creativity. In addition, these entertaining exercises often have deep connections to mathematics, which helps explain why many professional mathematicians start out as youngsters fascinated with puzzles.
In Mathematical Brain Teasers and Logic Puzzles, award-winning teacher and puzzle master Dr. Jason Rosenhouse, Professor of Pure Mathematics at James Madison University, introduces you to a selection of his all-time favorite mind-benders, including some going back to his childhood. Practically all of his 12 half-hour lessons start with a relatively simple problem that demonstrates a mathematical idea or problem-solving strategy. From there, you head deeper into the weeds, venturing into territory that will give you hours of challenging cogitation. While these puzzles can feel complicated on the surface, actually, no skills beyond middle school math are required.
Test Your Wits, Logic, and Persistence
Professor Rosenhouse starts the course by noting that despite all the difficulties humans face, they delight in inventing new problems solely for the pleasure of solving them. After speculating why that might be, he gets down to business—and fun. He introduces several classic puzzles that led to entirely new fields of mathematics. For example, in the 18th century, the city of Königsberg in Prussia had seven bridges connecting two islands with the surrounding city. Curious minds wondered whether it was possible to undertake a walk around Königsberg in such a way as to cross each bridge exactly once. With two islands to worry about and with so many possible walks, this problem is hard to solve just by walking around the city. The great mathematician Leonhard Euler finally answered the question, and in the process laid the foundation for graph theory.
Suitably inspired, you will plunge into more accessible—but no less beguiling—problems, including puzzles like these:
Original Outside-the-Box Puzzle: Nine dots arrayed in a square form the iconic outside-the-box puzzle. The goal is to connect all the dots with four straight lines without lifting your pencil from the page. In fact, by thinking really outside the box, it’s possible to connect the dots with just three lines.
140 Legs in a Barn: A barn holds a combined total of 50 chickens and horses. Altogether there are 140 legs. How many chickens and how many horses are there? You may be tempted to use algebra to reach a solution, but there is a much simpler way you can do quickly in your head. Can you see it?
Can Logic Get You into Heaven? You face two unmarked doors: one leading to heaven, the other to hell. A guard stands in front of each door. One is an always truthful knight, the other an always deceitful knave. You don’t know which is which. What single yes/no question can you ask to reveal the door to paradise?
Monty Hall Problem: Professor Rosenhouse analyzes the probability of different versions of the famous Monty Hall problem, in which the quizmaster of Let’s Make a Deal offers you a chance to switch your original choice after he reveals hidden information. A new car hinges on your decision!
Wolf, Goat, Cabbage: You must transport a wolf, a goat, and a cabbage across a river. You can carry only one of them at a time. However, the wolf will eat the goat if they are left unattended. Likewise, the goat will eat the cabbage. This puzzle is 1,200 years old, but its solution reflects the sort of algorithmic thinking underlying modern computer science.
The Joy of Figuring It Out
You also confront the so-called “Hardest Logic Puzzle Ever,” which lives up to its name. You delve into brain teasers devised by the celebrated Raymond Smullyan, inventor of “knights and knaves” and other logic challenges. You dip into Lewis Carroll’s diverting exercises in Aristotelian logic. You get to the heart of the paradoxical Tuesday birthday problem. You discover the connection between a horse on a treadmill and transcontinental air travel. You put yourself in the shoes of muddy-faced children who must determine, without mirrors or other obvious clues, that their faces are indeed muddy. And much more.
Professor Rosenhouse also provides useful tips for solving puzzles, including this observation for the muddy children problem: “Sometimes you have more information than you think. With careful attention to detail and a lot of patience and clear thinking, you can accomplish quite a lot from a very minimal starting point.” That’s good advice for any problem in life!
Throughout Mathematical Brain Teasers and Logic Puzzles, you learn useful ideas in mathematics and logic, such as:
Conditional and biconditional statements;
Coercive logic;
Conditional probability;
Why multiplying two negative numbers gives a positive result;
Bayes’ theorem;
Algorithmic thinking, and many other concepts.
But the biggest payoff is sheer joy. “A well-crafted puzzle or a clever brainteaser can be a lot of fun,” says Professor Rosenhouse, “and when you solve one, it can bring a smile to your face for the rest of the day.”
(Answer to the puzzle in the first paragraph: The man was buying house numbers. He paid 75 cents for numbers 1, 0, and 0. For solutions to the other puzzles, watch Mathematical Brain Teasers and Logic Puzzles. You’ll be inspired and amazed!)